
- #Simple shear and moment diagrams for free#
- #Simple shear and moment diagrams how to#
- #Simple shear and moment diagrams download#
This example uses the solve keyword with the Symbolic Evaluation Operator to derive the functions for reactions.ĭefine values for span, loading, and the range variable, z, which will set the points to plot. Similar to the previous examples, create functions for the reactions, and then create functions for shear and moment. This final example derives the functions for a triangular loading. In order to create the plots, define the values for span, load, and distance, and then create a range variable for the points to plot. Now that the equations for a point load are written, calculate and plot the shear and moment diagrams using the XY plot features.
#Simple shear and moment diagrams how to#
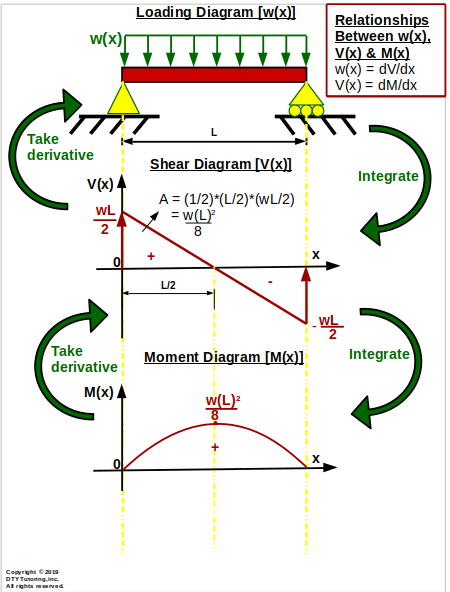
For this example, I use the keyword solve with the Symbolic Evaluation Operator to demonstrate how to solve for R A. Ignore the beam weight for this exercise. Create functions to describe the loading, shear, and moment. Let's now create shear and moment diagrams for a point load, P, placed anywhere along the beam at a distance "a" from the left end. Define values of span and uniform load, and the range variable, z, which will set the points to plot. The equation for shear or moment will be on the y-axis. Type the first value, then type a comma and enter the second value, which sets the step size. The range variable is defined by a starting value with the second value setting the step size. In order to create the plots, define the values for span and load, and then create a range variable for the points to plot. Select XY Plot from the Insert Plot button. Insert the plot from the Plots menu in the Traces section. Now that the equations are written, calculate and plot the shear and moment diagrams using the XY plot features. Now, write a function for the moment at a distance x by summing the moments about x. The shear at a distance x from the left is equal to the left reaction less the load applied to the beam between the left and the distance x (w*x).

Next, write a function for shear at a distance x by summing the vertical loads. It provides a symbolic solution rather than a numeric solution. The right arrow in the below functions is the Symbolic Evaluation Operator from the Symbolics section on the Math tab. Because Mathcad is unit aware, the span and load can be in any units of length and force. The variable "Span" is the length of the beam, and the variable "w" is a uniform load (force/length) along the length of the beam.

A clockwise moment will be considered positive. Once these functions are written, the results will be tested. Let's first calculate the left reaction, R A, by summing the moment about point B, and then calculate the right reaction, R B, by summing the vertical loads.

#Simple shear and moment diagrams download#
If you download the linked Mathcad file and double click on the figure it will open in PowerPoint. The figures in this blog were created in Microsoft PowerPoint as embedded objects. So, first, let's create some functions to help solve for and plot the shear and bending moment diagrams for a uniformly loaded, simply supported beam. I am a proponent of creating functions so that they can be used multiple times, rather than just solving a single problem. In this blog, I will show how to do this for simply supported beams with varying loading conditions. Mathcad can be used to calculate shears and moments and also draw the shear and bending moment diagrams. In this blog and several that follow, I will discuss how Mathcad can be used to calculate, plot, and derive these relationships.ĭrawing shear and bending moment diagrams of simply supported beams is one of the tasks in a basic engineering statics course. The deflection is a result of the loading, which is related to the shear, the bending moment, the beam slope, and the beam deflection. Similarly, as you walk across the floors in your home, the beams or joists deflect under your weight.
#Simple shear and moment diagrams for free#
If you need a Mathcad Prime worksheet viewer, download Mathcad Prime for free here.Ī truck driving on a bridge causes the supporting beams to deflect, resulting in various stresses in the beams. For the best reading experience, please download the Mathcad Prime 8 worksheet here. Editor's note: This blog article was originally written as a PTC Mathcad Prime worksheet.


 0 kommentar(er)
0 kommentar(er)
